wpk.2 Gravitation und Bewegung

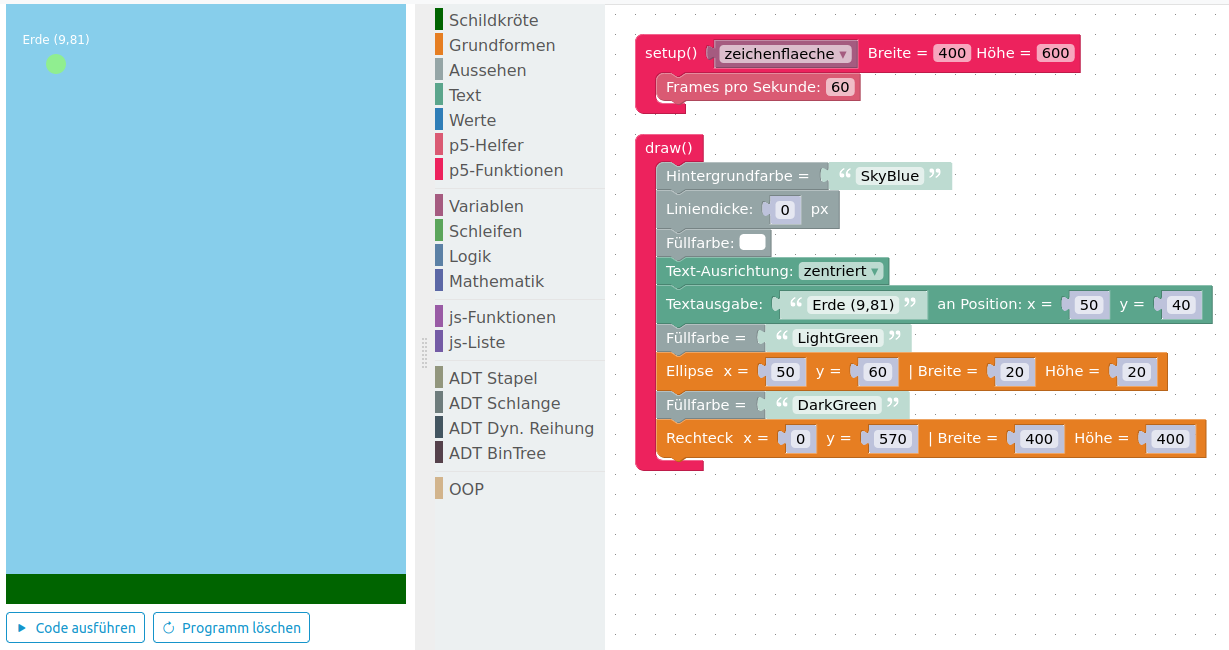
Mit dem Newtonschen Gravitationsgesetz und der Einsicht, dass eine Kraft den Bewegungszustand eines Körpers ändert, kann man das Verhalten der Himmelskörper vorhersagen.

Die Bewegung unter dem Einfluss von Gravitation kann berechnet werden. Vor der Zeit moderner Computer war dieses Unterfangen unsäglich aufwändig. Berechnungen mussten monatelang von Hand durchgeführt werden. Computer verkürzen heute die Zeit für notwendige Berechnungen auf einen Bruchteil der früher dafür benötigten Zeit.

In diesem Kapitel wird der freie Fall eines Apfel modelliert, mit der Annahme, dass sich während des Falls die Gravitation nicht messbar ändert. Bei der Modellierung können Sie die Kompetenzen anwenden, welche Sie im ersten Halbjahr in Informatik gelernt haben.

Die Erde wird als Rechteck dargestellt und der Apfel durch einen Kreis.

  • Laden Sie das Programm Apfel und Erde und machen Sie sich mit dem Aufbau vertraut.

  • Erweitern Sie das Programm so, dass der Apfel mit konstanter Geschwindigkeit auf die Erde fällt.

Apfel und Erde

Löst man die Formel \(v = \frac{s}{t}\) nach dem Weg \(s\) auf, so folgt:

\[ s = v \cdot t\]

Legt man für alle beteiligten Größen Variablen fest und vergrößert den Wert der Zeitvariablen in jedem Frame um 1, dann kann die Bewegung des Apfels mit konstanter Geschwindigkeit modelliert werden:

  • Laden Sie das Programm Apfel fällt mit konstanter Geschwindigkeit und machen Sie sich mit dem Aufbau und der Funktionsweise vertraut.

  • Erweitern Sie das Programm so, dass der Apfel mit konstanter Beschleunigung auf die Erde fällt.

Apfel fällt mit konstanter Geschwindigkeit

Wenn der simulierte Apfel mit konstanter Beschleunigung \(a\) in Richtung Erde fällt, gilt für die zurückgelegte Strecke:

\[ s = 0.5 \cdot a \cdot t^2\]

\(s = \text{beim freien Fall zurückgelegte Strecke}\)
\(a = \text{Fallbeschleunigung auf der Erde} = 9,81 \frac{\text{m}}{\text{s}^2}\)
\(t = \text{die während des Falls verstreichende Zeit}\)

Apfel fällt mit konstanter Beschleunigung

  • Erweitern Sie die Simulation so, dass im direkten Vergleich nebeneinander der freie Fall simuliert wird, wie dieser bei gleichem Zeitraffer auf mind. 5 Himmelskörpern unseres Sonnensystems beobachtet werden könnte.

  • Beschriften Sie jeden Apfel mit dem Namen des solaren Himmelskörpers und der dortigen Fallbeschleunigung.